NBHM Problem...

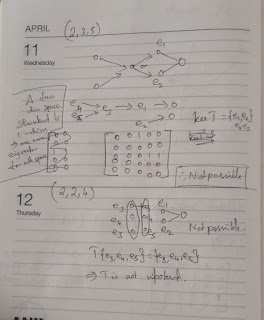
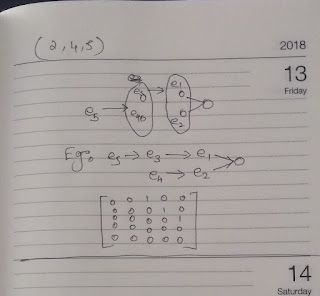
Let T be a nilpotent linear operator on the vector space $\mathbb{R}^5$ (i.e., $T^k=0$ for some k). Let $d_i$ denote the dimension of the kernel of $T^i$. Which of the following can possibly occur as a value of $(d_1,d_2,d_3)$? 

1.(1,2,3)
2.(2,3,5),
3.(2,2,4),
4.(2,4,5)

For the excellent proof using Jordan Canonical form visit https://nbhmcsirgate.theindianmathematician.com/2020/04/nbhm-2020-part-c-question-26-solution.html#.XqCM3QR0R10.whatsapp

Here we present a proof (incomplete in preciousness) on the fact "A linear transformation is completely determined by its behaviour on a basis."